Have you ever asked yourself what monoids and monads are, and particularly why they seem to be so attractive in the field of large-scale data processing? Twitter recently open-sourced Algebird, which provides you with a JVM library to work with such algebraic data structures. Algebird is already being used in Big Data tools such as Scalding and SummingBird, which means you can use Algebird as a mechanism to plug your own data structures – e.g. Bloom filters, HyperLogLog – directly into large-scale data processing platforms such as Hadoop and Storm. In this post I will show you how to get started with Algebird, introduce you to monoids and monads, and address the question why you should get interested in those in the first place.

Goal of this article

The main goal of this is article is to spark your curiosity and motivation for Algebird and the concepts of monoid, monads, and category theory in general. In other words, I want to address the questions “What’s the big deal? Why should I care? And how can these theoretical concepts help me in my daily work?”

While I will explain a little bit what the various concepts such as monoids are, this is not the focus of this post. If in doubt I will rather err on the side of grossly oversimplifying a topic to get the point across even at the expense of correctness. There are much better resources available online and offline that can teach you the full details of the various items I will discuss here. That being said, I compiled a list of references at the end of this article so that you have a starting point to understand the following concepts in full detail, and with more accurate and thorough explanations than I could come up with.

Motivating example

A first look at Algebird

Here is a simple example what you can do with monoids and monads, based on the starter example in Algebird.

scala> Max(10) + Max(30) + Max(20)
res1: com.twitter.algebird.Max[Int] = Max(30)

// Alternative, Java-like (read: ugly) syntax for readers unfamiliar with Scala.
scala> Max(10).+(Max(30)).+(Max(20))
res2: com.twitter.algebird.Max[Int] = Max(30)

What is happening here? Basically, we are boxing two numbers, the Int values 4 and 5, into Max, and then we are “adding” them. The behavior of Max[T] turns the + operator into a function that returns the largest boxed T.

Conceptually this is similar to the following native Scala code:

// This is native Scala.
scala> 10 max 30 max 20
res3: Int = 30

// Alternative, Java-like syntax.
scala> 10.max(30).max(20)
res4: Int = 30

At this point you may ask, “Alright, what is the big deal? The native Scala example looks actually better!”

At least, that is what I thought myself at first. But the simplicity of this example is deceptive. There is a lot more to it than meets the eye at first sight.

Beyond trivial examples

Admittedly, the first example used a very dull data structure, Int. Any programming language comes with built-in functionality to add two integers, right? So you would be hardly convinced of the value of a tool like Algebird if all it allowed you to do was 4 + 3 = 7, particularly when doing those simple things would require you to understand sophisticated concepts such as monoids and monads. Too much effort for too little value I would say!

So let me use a different example because adding Int values is indeed trivial. Imagine that you are working on large-scale data analytics that make heavy use of Bloom filters. Your applications are based on highly-parallel tools such as Hadoop or Storm, and they create and work with many such Bloom filters in parallel. Now the money question is: How do you combine or add two Bloom filters in an easy way? (This is where monoids come into play.)

val first = BloomFilter(...)
val second = BloomFilter(...)
first + second == uh?

And what about performing other operations on those Bloom filter instances, notably data processing pipelines based on common functions such as map, flatMap, foldLeft, reduceLeft? (And this is where monads come to into play.)

val filters = Seq[BloomFilter](...)
val summary = filters flatMap { /* magic happens here */ } reduceLeft { /* more magic */ } ...

And what about combining two HyperLogLog instances?

Intuitively we could say that the general idea of “adding” two Bloom filters is quite similar to how we would add two sets A and B, where adding would mean creating the union set of A and B.

Now Algebird addresses this problem of abstraction. In a nutshell, if you can turn a data structure into a monoid (or semigroup, or …), then Algebird allows you to put it to good use. You can then work with your data structure just as nicely as you are so used to when dealing with Int, Double or List. And you can use it with large-scale data processing tools such as Hadoop and Storm, too.

Wait a minute!

In case you are asking yourself the following question (which I did): Is the magic of Algebird simply something like a custom Max[Int] class that defines a +() method, similar to the following snippet but actually with a bounded type parameter T : Ordering[T]? (If you do not understand the latter, take a look at this StackOverflow thread.)

// Is Algebird implemented like this? (hint: nope)
scala> case class Max(val i: Int) { def +(that: Max) = if (this.i >= that.i) this else that }
defined class Max

scala> Max(10) + Max(30) + Max(20)
res5: Max = Max(30)

The answer is yes and no. “Yes” because it is similar. And “no” because the implementation is quite different from the above analogy, and provides you with significantly more algebra-fu (but again, it has the same spirit).

What we want to do

Our goal in this post is to build a data structure TwitterUser accompanied by a Max[TwitterUser] monoid view of it. We want to use the two for implementing the analytics of a fictional popularity contest on Twitter, like so:

// Let's have a popularity contest on Twitter.  The user with the most followers wins!
val barackobama = TwitterUser("BarackObama", 40267391)
val katyperry = TwitterUser("katyperry", 48013573)
val ladygaga = TwitterUser("ladygaga", 40756470)
val miguno = TwitterUser("miguno", 731) // I participate, too.  Olympic spirit!
val taylorswift = TwitterUser("taylorswift13", 37125055)

val winner: Max[TwitterUser] = Max(barackobama) + Max(katyperry) + Max(ladygaga) + Max(miguno) + Max(taylorswift)
assert(winner.get == katyperry)

Figuring out how to do this with monoids, monads, and Algebird is the objective of this article.

Of course, instead of using Algebird and monoids we could also project the number-of-followers field from each user and perform any such analytics directly on the Int values. That’s not the point however. I intentionally wanted a very simple example use case because, as you will see, there is so much to understand about what’s going on behind the scenes that any further distraction should be avoided. At least, that was my personal experience. :-)

My journey down the rabbit hole

This section is more for entertainment. Feel free to skip it.

How this post started

I am following a few Twitter folks on, well, Twitter such as Dmitriy Ryaboy (@squarecog) and Oscar Boykin (@posco). And lately they talked a lot about how data analytics at Twitter is powered by “monoids” and “monads”, and how tools such as Algebird and Scalding form the code foundation of their analytics infrastructure.

Here is an example of such a conversation:

Monads. Monads everywhere!

A mo-what? And how comes those things are apparently spreading like a contagious disease throughout their data analytics code?

Another trigger was a discussion involing Ted Dunning of MapR (@ted_dunning) and his work on a new data structure called t-digest:

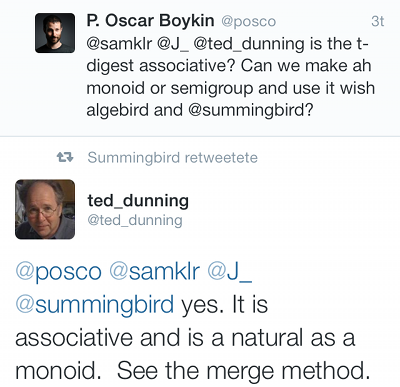
Is t-digest associative?

Why was Ted being asked whether t-digest is associative? And how does all this relate to semigroups and monoids? And finally, what the heck are semigroups in the first place?

Now a dangerous series of events began to take place on my side.

First I thought, “Hey, coincidentally I have started to pick up Scala around a month ago. Given that Algebird is written in Scala this might turn into an interesting finger exercise.” (Note my focus on “finger exercise”.) On top of that I knew that the use of Algebird extends to other interesting big data tools such as Storm and Scalding, so it could turn out that I would not only learn something for learning’s sake but that I could put it to practical use in my daily work, too. The combination of these two factors – general interest and practical applicability – eventually caused me to give in to my curiosity and decided to put “an hour or two aside” to read up on those monoid thingies and figure out whether and how I could leverage Algebird for my own purposes.

You might notice at this point that it all started quite innocently. But what I did not realize at that moment was that I was opening Pandora’s box on an otherwise quiet and peaceful Swiss weekend…

Scala, functors, monoids, monads, category theory, implicits, type classes, aaargh!

What started as a seemingly innocent journey down a calm park lane quickly turned into the opening of the gates of functional programming and category theory hell. Not only did I struggle to understand what things like functors, semigroups, monoids, and other algebraic structures that only a mother could love are. No, on top of that I quickly realized that how these things can be implemented in Scala in general and in Algebird in particular meant I had to take my beginner Scala-fu to a whole new level. In the end it took me the full weekend to grasp all those concepts to the point where I’d say right now that I know enough to be dangerous.

The learning curve reminded me a lot of the following famous picture:

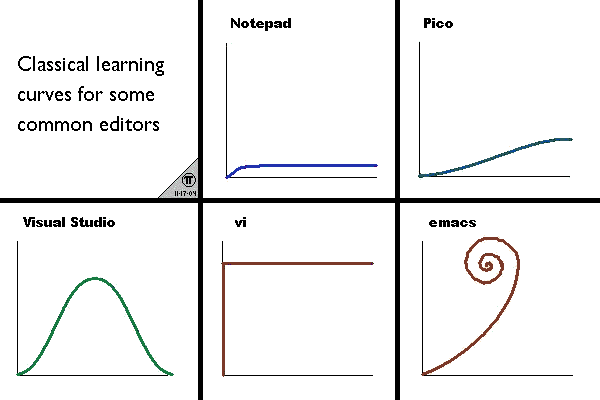
Learning curve for some common editors

Figure 1: Learning curve for some common editors. Image courtesy of Jose M. Gilgado.

And it did feel like the vi curve – the brick wall experience. What else could it be, right? That being said I still fear that, after having hit and finally made it over that initial brick wall, it may still spiral out of control again like the Emacs curve. :-)

Picture myself sitting in front of my keyboard, frantically interacting with your favorite search engine, StackOverflow, Wikipedia, your usual suspects of Scala books, and what not:

Me: “What is a monad?”

Internet: “A monad is just a monoid in the category of endofunctors.”

Me: “Hmm, ok. So what is a monoid?”

Internet: “A monoid is a semigroup with identity.”

Me: “Then what is a semigroup??” (number of question marks increases with anxiety level)

Internet: “An algebraic structure consisting of a set together with an associative binary operation.”

Me: “Alright, I see the mathematical definition and I do see a soup of greek letters. Still, what is it? Where can I get one from, and what can I use it for?”

Internet: “Here is an example in the Haskell programming language.”

Me: <censored>

On a more serious note, the past few days have really been a tour de force where I felt I would recursively dive from one new term or concept into yet more new terms and concepts, to the point where my brain would run into a stack overflow. “Why am I actually reading about magmas, or co- and contra-variance in Scala, or bounded type parameters? What was the original question I tried to find an answer for?”

To make a long story short I was really deep down the rabbit hole, with no Alice in sight but fully surrounded by semigroups of monoidal and diabolical jabberwockies on a big night out. Given the questions, comments and blog posts of other folks at least I found consolation in the fact that I was apparently not alone.

And, finally, at the end of the hole there was a bit of light. In the next sections I want to share what I have learned so far in the hope that it will prove helpful for you, too. We start with a brief introduction to monoids and monads, followed by how to apply what we have learned in Algebird hands-on.

The TL;DR version of monoids and monads

Michael’s abridged relation of monoids and monads: A monad is a monoid where you blend the “oi” into an “a”. Depending on your typesettings (pun intended) this blend will be easier or harder for you to see. If in doubt, squint more.

As a grossly simplified rule of thumb:

  1. Monoid: If you want to “attach” operations such as +, -, *, / or <= to data objects – say, adding two Bloom filters – then you want to provide monoid forms for those data objects (e.g. a monoid for your Bloom filter data structure). This way you can combine and juggle your custom data structures just like you would do with plain integer numbers.
  2. Monad: If you want to create data processing pipelines that turn data objects step-by-step into the desired, final output (e.g. aggregating raw records into summary statistics), then you want to build one or more monads to model these data pipelines. Particularly if you want to run those pipelines in large-scala data processing platforms such as Hadoop or Storm.

The intent of this section is to give you a high-level idea what those concepts are, and what you can use them for. That is, this section should help you determine whether you want to venture down the rabbit hole, too.

I did not want to add yet another variant to the pool of “what is a monoid/monad” articles, but at the same time I felt I need to explain at least very briefly what the various concepts are (as good as I can) so that you can better understand how to use a tool such as Algebird.

Of course, if you ran across a blatant mistake on my side please do let me know!

Monoids

What is a monoid?

A monoid is a structure that consists of:

  1. a set of objects (such as numbers)
  2. a binary operation as a method of combining them (such as adding those numbers)

The small catch is that the way you can combine the objects in your set must adhere to a few rules, which are described in the next section.

One way to explain a monoid in the context of programming is as a kind of adapter or bounded view of a type T. Imagine a data structure of type T – say, a List. If you can find a way to use T in a way that conforms to the monoid laws (see next section), then you can say “type T forms a monoid” Monoid[T]; for instance, if the binary operation you picked behaves like the concept of addition, you have an additive monoid view of T.

Note: What I tried to highlight in the previous paragraph is that a given type T can have multiple monoidal forms. An additive monoid of T is just an example, and T might have more monoids than the additive variant. Also -- sorry for the forward reference -- a type T can form both a monoid and a monad. One such dual-headed hydra is the well-known List.

So you can read Monoid[T] as “T looks like a monoid and quacks like a monoid, so it must be a monoid”. This notion is related to the concept of duck typing in languages such as Python. Scala, in which Algebird is implemented, has a static type system though, and to achieve such ad-hoc polymorphism we typically use type classes to achieve a similar effect. A nifty feature of type classes is that they allow you to retroactively add polymorphism even to existing types that are not under your own control: examples are Seq or List, which are provided by the Scala standard library and thus not under your control.

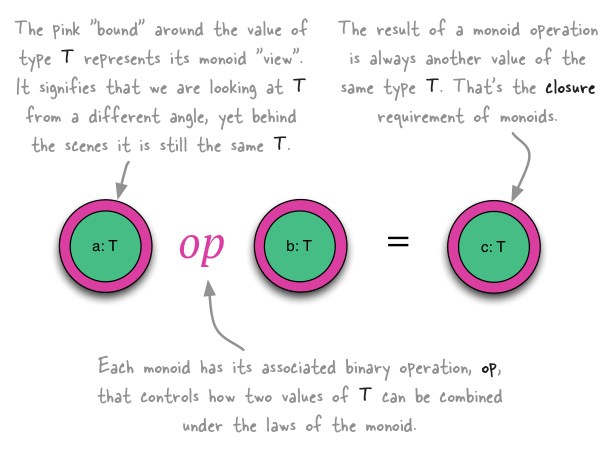
Monoid illustration

Figure 2: A monoid seen as a bounded view. In this analogy we are looking at the original type T from a different, "monoidal angle". Here, we are combining two values of type T under the laws of the pink-colored monoid view of T (whatever this particular monoid might actually be doing).

Monoids in more detail

A monoid is a set of objects, T, together with a binary operation ⋅ that satisfies the three axioms listed below.

One way to express a monoid in Scala would be the following trait, used as a type class:

// Important: What you see here is only part of the contract.
// The monoid, and thus `e` and `o`, must also adhere to the monoid laws.
trait Monoid[T] {
  def e: T
  def op(a: T, b: T): T
}
Closure
For all a, b in T, the result of the operation a ⋅ b is also in T: $$ \forall a,b \in T: a \bullet b \in T $$ In Scala, we could express this axiom with the following function signature for ⋅: def op(a: T, b: T): T
Associativity
For all a, b, and c in T, the equation (a ⋅ b) ⋅ c = a ⋅ (b ⋅ c) holds: $$ \forall a,b,c \in T: (a \bullet b) \bullet c = a \bullet (b \bullet c) $$ In Scala, we could express this axiom with: (a op b) op c == a op (b op c)
Identity element
There exists an element e (we could also call it zero to draw a link to addition) in T, such that for all elements a in T, the equation e ⋅ a = a ⋅ e = a holds: $$ \exists e \in T: \forall a \in T: e \bullet a = a \bullet e = a $$ In Scala, we could express this axiom with the following, which as you might note captures the idea of a no-op: e op a == a op e == a
Note: Any binary operation satisfying the three axioms above qualifies your data structure to be a monoid. It does not necessarily need to be an addition-like operation.

Before we move on and look at examples of monads, I want to mention one more thing about the binary function of a monoid. We have learned that it must be associative. Wouldn’t it be helpful if the binary function were commutative, too, even though this optional feature would not be required to make a monoid?

Here is a transcripted reply during Sam Ritchie’s SummingBird talk at CUFP:

Question: Associativity is one nice thing about monoids, but what about commutativity [which] is also important. Are there examples of non-commutative datastructures

Answer: It should be baked into the algebra (non-commutativity). This helps with data skew in particular. An important non-commutative application is Twitter itself! When you want to build the List monoid, the key is userid,time and the value is the list of tweets over that timeline (so ordering matters here). It’s not good to get a non-deterministic order when building up these lists in parallel, so that’s a good example of when associativity and commutativity are both important.

Source: Transcript of Sam Ritchie’s SummingBird talk at CUFP 2013

What are example monoids?

  • Numbers (= the set of objects) you can add (= the method of combining them).
    • For integer addition, e == 0 and op == +.
    • For integer multiplication, e == 1 and op == *.
  • Lists you can concatenate.
    • With e == Nil and op == concat.
  • Sets you can union.
    • With e == Set() and op == union.

There are more and also more sophisticated examples, of course. Max[Int] at the beginning of this article is a monoid, too.

Here is how Algebird defines an additive monoid for the standard type Seq:

// A `Seq` concatenation monoid.
// Plus (the `op`) means concatenation,
// zero (the identity element `e`) is the empty Seq.
class SeqMonoid[T] extends Monoid[Seq[T]] {
  override def zero = Seq[T]()
  override def plus(left : Seq[T], right : Seq[T]) = left ++ right
}

// Make an instance of `SeqMonoid` available as an implicit value.
// This is a Scala-specific implementation action that needs to be done,
// i.e. it is not related to the abstract concept of monoids.
//
// The effect of this statement is to add the "monoid view" of Seq
// as defined above to all `Seq` instances in the code.  If you
// define your own monoid for a type `T` in Algebird and forget
// this statement, Algebird will complain with the following
// @implicitNotFound error message:
//
//   "Cannot find Monoid type class for T"
//
// Implicits need to be used because this is how the notion of
// type classes is implemented in Scala.
implicit def seqMonoid[T] : Monoid[Seq[T]] = new SeqMonoid[T]

Algebird actually includes a few more methods for the Monoid[T] type class – which SeqMonoid[T] extends – but the key functionality is shown above.

What can I use a monoid for? Why should I look for one?

Whenever you have a data structure (which backs your “set of objects”, e.g. the Int data structure or the List[T] data structure) you can begin checking whether you can define one or more monoids for that data structure. Here you will start looking for operations you can perform on any two instances of your data structure that satisfy the three monoid axioms: closure, associativity, and identity element (the latter gives your monoid a no-op function, and is the one thing that turns a semigroup into a monoid).

If you do find any such monoids for your data structure, hooray! On the practical side this means means that you can now use your data structure in any code that expects a monoid. As I said above you can think of a monoid as an adapter, or shape, for (some monoid-compatible aspects of) your data structure that allows you to fit your data structure peg into a monoid hole. Some such holes are Algebird, Scalding and Summingbird of Twitter. Being supported by those tools also means that you can now plug your data structure into big data analytics tools such as Hadoop and Storm, which might be a huge seller and productivity gain for your new data structure.

If your data structure has a monoid form, this means you can plug the data structure directly into large-scale data processing platforms such as Hadoop and Storm. Secondly, and in more general terms, it signifies because of the associativity of monoid operations that those operations on your data structure can be parallelized in order to utilize multiple CPU cores efficiently. Speaking in code, that means you can run operations such as foldLeft() and reduceLeft() on them. And parallelization support is yet another reason why monoids (and monads) are so attractive for big data tools such as Hadoop and Storm, where your code not only runs on many cores per machine but on many such machines in a cluster. In other words: If your data structure has a monoid form, this means you can plug the data structure directly into large-scale data processing platforms such as Hadoop and Storm. Hence monoids enable you to MapReduce and to divide and conquer.

Let me quote Sam Ritchie (@sritchie), former Twitter engineer and now founder of PaddleGuru (cool idea, by the way – go sports!) for a very concrete practical application of monoids at Twitter. Well, actually I am quoting a transcript of his talk.

One cool feature: When you visit a tweet, you want the reverse feed of things that have embedded the tweet. The MapReduce graph for this comes from: When you see an impression, find the key of the tweet and emit a tuple of the tweetId and Map[URL, Long]. Since Maps have a monoid, this can be run in parallel, and it will contain a list of who has viewed it and from where. The Map has a Long since popular tweets can be embedded in millions of websites and so they use a “CountMinSketch” [Note: Reader Sam Bessalah points out that the transcript is wrong when it said “accountment sketch”.] which is an approximate data structure to deal with scale there. The Summingbird layer which the speaker [Sam Ritchie] shows on stage filters events, and generates key-value pairs and emits events.

Twitter advertising is also built on Summingbird. Various campaigns can be built by building a backend using a monoid that expresses the needs, and then the majority of the work is on the UI work in the frontend (where it should be — remember, solve systems problems once is part of the vision).

Source: Transcript of Sam Ritchie’s SummingBird talk at CUFP 2013

See his CUFP slides on Summingbird for further detail.

Thirdly, you can compose monoids. For instance, you can form the product of two monoids M1 and M2, which is the tuple type (M1, M2). This product is also a monoid.

Lastly, you can now combine your monoidal data structure with monads (see below) and benefit from all the features that those monads provide.

At this point you might guess the reason why Ted Dunning was asked whether the t-digest data structure he is working on is associative and can be turned into a semigroup or monoid. One of my two mysteries solved!

Monads

What is a monad?

Update: A few readers pointed out that this section explains rather what monads are used for than what they really are. I concur! And I even skip a discussion of Monad laws etc. intentionally because the post is already quite long, and the focus and motivation of this article (see above) is not an in-depth introduction to monoids or monads. It's about the questions "Why should I be interested in the first place, and what can I use them for?". Of course I can understand the need for further details, so I added a list of references and literature to the end of this article, which you can read at your leisure. Of course if you think that some important piece of information should be mentioned here directly (or something happens to be plain wrong), please let me know. It's difficult to write an article about such a topic in a way that can be understood by beginners and at the same time also pleases the experts.

A monad is a structure that defines a way to combine functions. It represents computations defined as a sequence of transformations that turn an original input into a final output, one step at a time. Think of them like function chaining similar to y = h(g(f(x))).

An interesting aspect is that in the case of a monad the type of the value being piped through the function chain may change along the way. For instance, you may start with an Int but end up with a Double or BloomFilter. This is different from a monoid, which will always retain the original type because of the closure requirement (see monoid laws above).

One of the best analogies for monads I found is the following, adapted from Wikipedia: You can compare monads to physical assembly lines, where a conveyor belt (the monad) transports a piece of input material (the data) between functional units (functions on the data) that transform the piece one step at a time. Think of the skeleton of a car that is turned into the final car in a sequence of steps. Or of web server log files with raw data that is turned into business information such as the increase of ad impressions in the EMEA market for this month.

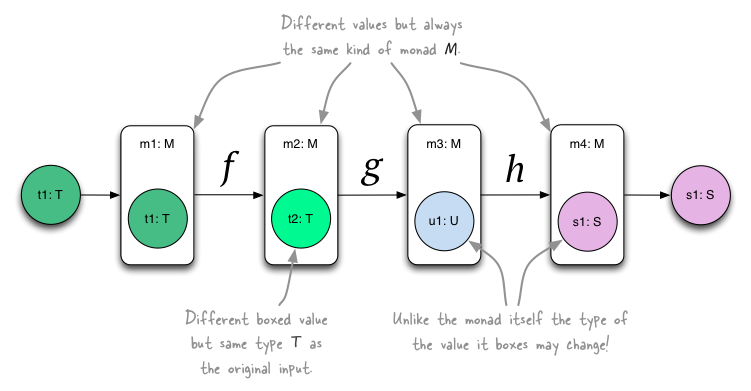
Monad data processing pipeline

Figure 3: A monad seen as a data processing pipeline. The monad M is used to turn the original input into the final output one step at a time.

Sticking with this analogy, a monad enables you to decorate each processing step in the assembly pipeline with additional context (or an “environment”). For instance, your monad could carry state information that is used by the functions in the pipeline – this would be the example of a state monad. Alternatively, your monad could log what is going on before, within, or after a function to a file or database – this would be the example of an I/O monad. If you are a game developer, you could use a monad to carry the representation and state of the game environment (such as the current level), and the functions in the pipeline would model how players can interact with the environment.

Before we look at monads in more detail, let us take a brief detour to Storm. When you are implementing bolts in Storm – i.e. Storm’s version of the “functional units” in a data processing pipeline – you will come across the prepare() and execute() methods (see the Storm tutorial):

public class TripleBolt extends BaseRichBolt {
  private OutputCollectorBase collector;

  // Note how the Storm provides "context" -- a literal context value
  // and a collector value -- to the bolt as the functional unit in
  // the data processing pipeline.
  @Override
  public void prepare(Map conf, TopologyContext context, OutputCollectorBase collector) {
    this.collector = collector;
  }

  // This is Storm's version of a monad's `fn` function,
  // which we will discuss in the next section.
  @Override
  public void execute(Tuple input) {
    int val = input.getInteger(0);
    int tripled = val * 3;
    collector.emit(input, new Values(tripled));
    collector.ack(input);
  }

  // ...rest omitted...
}

Note how Storm provides environmental information and context to the bolt. This is one example where you could point your finger at the code and say, “This would be a good place to use a monad.” In this specific case I would say it would be primarily a kind of I/O-monad because the collector instance allows the bolt write its output to downstream bolts via network communication.

Monads in more detail

Here is one way to capture the concept of a monad in Scala. It is basically the same as the definition of a monad in Algebird.

// Important: What you see here is only part of the contract.
// The monad, and thus `apply` and `flatMap`, must also adhere to the monad laws.
trait Monad[M[_]] {
  // Also called `unit` (in papers) or `return` (in Haskell).
  def apply[T](v: T): M[T]

  // Also called `bind` (in papers) or `>>=` (in Haskell).
  def flatMap[T, U](m: M[T])(fn: (T) => M[U]): M[U]
}

Alright, what is going on here?

apply() boxes a T value into the monad M[T]. For example, T is an Int, the monad M[T] is a List[T]. In other words, it is a good-ol’ constructor for the monad.

flatMap() turns a T into a potentially different type parameter U (but it can also be a T again) that is boxed into the same type of monad M, i.e. M[U]. In plain English, this means that if you have List monad all it will ever produce for you is another List monad, but the type of elements in the List monad may change. The way this happens is controlled by the second parameter of flatMap(), which is a function from T to M[U].

For example, T is an Int, U is a Double, and M is a List monad; fn is (i: Int) => List(i.toDouble / 4, i.toDouble / 2), i.e. T -> M[U]. If you ran this combination over the input List[Int](1, 2), you would get the output: List[Double](0.25, 0.5, 0.5, 1.0).

Note how flatMap() provides the boxing M instance m of the input T value to the function fn via currying. This way fn may leverage information or functionality embedded in the monad, including functions beyond the contractually required flatMap(). One such example is Monad[Some], i.e. the Some monad in Algebird. The flatMap() function of this monad calls Some#get(), which is a function of Some but not of Monad[Some]. As such a monad is also a kind of adapter or view, similar to the way we described monoids above. If you still cannot see how similar monoids and monads are, just try squinting harder!

Similar to the monoid laws we discussed above, monads have their own laws – and these rules are actually very similar to its monoid brethren! I decided not to discuss monad laws in this post because I feel it is already very long. I may update the post at a later point though. In the meantime take a look at the following references:

  • Monad laws (in Haskell). Remember return in Haskell means our constructor apply() in Scala, and >>= in Haskell is our flatMap().
  • Monads are elephants, a series of blog posts by James Iry. In Scala.

I hope you will notice their similarities:

  • The identity rules of monads are similar to the identity element e of monoids.
  • Both monoids and monads have functions that must be associative.

What are example monads?

At the beginning of the section on monads I already mentioned the state-monad and the I/O-monad.

Well, this may still be a bit vague. Let us look at a more concrete (and maybe simpler) example. Any collection type is typically a monad. For example, take List[T]:

  • The constructor of List[T] acts as unit as it gives you a List[T] box for T instances.
  • List has an appropriate flatMap() function – and map(), which can be built from flatMap() and the constructor.

Here is the implementation of Monad[List] in Algebird:

implicit val list: Monad[List] = new Monad[List] {
  def apply[T](v: T) = List(v);
  def flatMap[T,U](m: List[T])(fn: (T) => List[U]) = m.flatMap(fn)
}

Here you can see that Monad[List] is simply a 1:1 adapter for the existing apply() and flatMap() functions of List. And that’s because List in Scala already ships with monad “look and feel”.

Before we move on to the next section there is one more interesting facet: A monad can have monoid forms, too. Algebird, for instance, provides a default monoid view for its semigroups and monads:

// This is a Semigroup, for all Monads.
class MonadSemigroup[T,M[_]](implicit monad: Monad[M], sg: Semigroup[T])
  extends Semigroup[M[T]] {
  import Monad.operators
  def plus(l: M[T], r: M[T]) = for(lv <- l; rv <- r) yield sg.plus(lv, rv)
}

// This is a Monoid, for all Monads.
class MonadMonoid[T,M[_]](implicit monad: Monad[M], mon: Monoid[T])
  extends MonadSemigroup[T,M] with Monoid[M[T]] {
  lazy val zero = monad(mon.zero)
}

Groups, rings, and fields do not have such a default, “automatic” monoid view however. For those algebraic structures you must check yourself that the group/ring/field laws hold for your monad.

What can I use a monad for? Why should I look for one?

As we have already seen monads can be thought of as composable computation descriptions. This means you can use them to build powerful data processing pipelines. And these pipelines are not only powerful in terms of features and functionality, they can also be parallelized, which is one of the reasons why monads are so attractive in the field of large-scale data processing where your code is run on many cores and on many machines at the same time.

Now you might say that almost all we do in coding is to transform one value into another value, and I agree. And this, I think, is where the idea of the picture "Monads. Monads, everywhere." (see beginning of this article) originates from. Two of my two mysteries solved, yay!

Algebird

Finally we are getting close to being productive with Algebird. I figure the previous TL;DR section on monoids and monads was still maybe a bit too long. :-)

If you recall, our original goal at the beginning of this post was to build a data structure TwitterUser accompanied with a Max[TwitterUser] monoid view of it, using Algebird. We wanted to use the two for implementing the analytics of a simple popularity contest on Twitter:

// Let's have a popularity contest on Twitter.  The user with the most followers wins!
val barackobama = TwitterUser("BarackObama", 40267391)
val katyperry = TwitterUser("katyperry", 48013573)
val ladygaga = TwitterUser("ladygaga", 40756470)
val miguno = TwitterUser("miguno", 731) // I participate, too.  Olympic spirit!
val taylorswift = TwitterUser("taylorswift13", 37125055)

val winner: Max[TwitterUser] = Max(barackobama) + Max(katyperry) + Max(ladygaga) + Max(miguno) + Max(taylorswift)
assert(winner.get == katyperry)

Let’s start!

Creating a monoid

The TwitterUser type

Our first step is to create the data structure TwitterUser for which we will then create a monoid view.

Because we want to build a Max monoid for TwitterUser eventually, we must come up with a way to order TwitterUser values. For this we can either use the Ordering or the Ordered trait in Scala, either way will work.

Let’s say we go down the Ordered route. Now we must answer a design question: Do we consider the “ordering” behavior to be a defining feature of TwitterUser in general, or do we need this behavior only for its Max[TwitterUser] monoid view? If it’s a general feature we would add it to TwitterUser directly. If it’s only needed for the monoid we can also decide to add it only there. In our case, we will add the ordering behavior to TwitterUser directly. I will show further down below how to implement the other option.

// Small note: To be future-proof we should make `numFollowers` a `Long`,
// because `Int.MaxValue` (~ 2 billion) is less than the potential number
// of Twitter users on planet earth.  I am happy to let this one slip though.
case class TwitterUser(val name: String, val numFollowers: Int) extends Ordered[TwitterUser] {
  def compare(that: TwitterUser): Int = {
    val c = this.numFollowers - that.numFollowers
    if (c == 0) this.name.compareTo(that.name) else c
  }
}

The code above means that TwitterUser supports comparison operations like >= as defined by the compare method of the Ordered trait.

scala> TwitterUser("foo", 123) > TwitterUser("bar", 99999)
res5: Boolean = false

In our case this compare() method is also used as the monoidal binary function of the Max[TwitterUser] monoid we will build in the next section. This works because compare() satisfies all the three axioms described in our section on monoids above.

The Max[TwitterUser] monoid

Creating the Max monoid for TwitterUser is now very simple because we can leverage a factory method provided by Algebird’s called Max.monoid().

// The "zero" element of the TwitterUser monoid.  Traditionally it is
// also called `mzero` in academic papers.  We use `Int.MinValue` here
// but in practice you would typically constrain `numFollowers` of
// TwitterUser to be >= 0 anyways, so any negative value such as `-1`
// would do.
val zero = TwitterUser("MinUser", Int.MinValue)

// Monoid in Algebird is a type class, hence we use implicits
// to make the monoid available to the rest of the code.
implicit def twitterUserMonoid: Monoid[Max[TwitterUser]] = Max.monoid(zero)

That’s it!

Ok, maybe it feels a bit like cheating because the monoid is created behind the scenes by Max.monoid(). So what does Max.monoid() do?

/* This is Algebird code, not ours. */

// Zero should have the property that it <= all T
def monoid[T](zero: => T)(implicit ord: Ordering[T]): Monoid[Max[T]] =
   Monoid.from(Max(zero)) { (l,r) => if(ord.gteq(l.get, r.get)) l else r }

Still, it’s pretty straight-forward I would say. Not a lot of magic as long as you know how implicits and type classes in Scala work.

Generally, Max in Algebird is a semigroup -- not a monoid -- because not all types T you could come up with would have the notion of a zero element when used with Max. And the existence of such a zero element is the one thing that separates a semigroup from a monoid. You see this in Algebird's OrderedSemigroup.scala where object Max defines an implicit def semigroup, and only for a few specific types such as Int or Long it also defines monoid behavior.. This is because those types have the notion of a zero element. In our case we have such a zero element, too, hence we can not only support semigroup but also monoid behavior.

What would we do if we only wanted to add compare() to the monoid, but not to the original type? The Algebird code has examples for this use case. Here is the definition of the Max[List] monoid, which as you may notice uses Ordering and not Ordered as in our example above. You can ignore that small difference. The key point is that the compare() method is defined as part of the Max[List] monoid instead of being “duct-taped” to List directly.

implicit def listMonoid[T:Ordering]: Monoid[Max[List[T]]] = monoid[List[T]](Nil)(new Ordering[List[T]] {
  @tailrec
  final override def compare(left: List[T], right: List[T]): Int = {
    (left, right) match {
      case (Nil, Nil) => 0
      case (Nil, _) => -1
      case (_, Nil) => 1
      case (lh::lt, rh::rt) =>
        val c = Ordering[T].compare(lh, rh)
        if(c == 0) compare(lt, rt) else c
    }
  }
})

Where to go from here?

Now that we have one monoid view for TwitterUser, what else can we do? Can we find another monoid form for it? That’s one of the questions you should ask yourself when working with your own data structures. If you take a look at the Algebird code, you will notice that many types such as List will have quite a few algebraic forms.

There is one more thing I want to mention here: You may consider creating an additive monoid for TwitterUser, i.e. a monoid that supports a + like operation. I couldn’t come up with any good example how the result of adding two such values would make sense (e.g., how could you “add” their usernames in meaningful way?). That being said there is one case where adding two TwitterUser values would make sense: to capture the idea that one follows the other, i.e. to create a relationship (a link) between the two. Keep in mind though that monoids and friends must adhere to the closure principle – if you start out with a TwitterUser value and perform monoid operations on it, the end result must always be another TwitterUser value. Of course such a relationship can be modeled in code, but you cannot do this with a TwitterUser monoid as defined above.

Creating a monad?

By now you should have sufficient understanding of monads and Algebird to implement your own monad. So I leave this as an exercise for the reader.

A starting point for you is Monad.scala in Algebird.

However if you do have a good idea what kind of monad I could showcase here – perhaps something related to Twitter to match the TwitterUser monoid example above? – please let me know in the comments.

Key algebraic structures in Algebird

The following table is a juxtaposition of a few key algebraic structures, notably those that are implemented in Algebird. It should help you to navigate the Algebird code base, and also to figure out which algebraic structure your own data types might support – i.e., “Can I turn my T into a semigroup, or even a monoid?”.

Algebraic structure Binary op is associative Identity (has a zero element) + op - op * op / op References
Semigroup YES - YES - - - Wikipedia, Algebird
Monoid YES YES YES - - - Wikipedia, Algebird
Group YES YES YES YES - - Wikipedia, Algebird
Ring YES YES YES YES YES - Wikipedia, Algebird
Field YES YES YES YES YES YES Wikipedia, Algebird

Think of + as the general notion of “adding one thing to another”, same for the other operations. For two List[Int], for instance, + could be concatenation of the two (instead of, say, trying to add the individual Int elements of the lists together). The operators +, -, * and / are as defined in Algebird.

A small Algebird FAQ

Error “Cannot find Group/Monoid/… type class for a type T”?

If you run into this error it means you are trying to use an operation that is not supported by the algebraic structure you are working with. In this specific example, a Set() in Algebird has a monoid form and thus supports an addition-like operation + but not a multiplication-like operation *.

scala> Set(1,2,3) * Set(2,3,4)
<console>:2: error: Cannot find Ring type class for scala.collection.immutable.Set[Int]
              Set(1,2,3) * Set(2,3,4)

Combine different monoids?

In theory you can combine different monoids such as Max[Int] and Min[Int] and form their product, but there must exist an appropriate algebraic structure for that product. Right now, for instance, the following code will not work in Algebird because it does not ship with a algebraic structure for (Max[Int], Min[Int]):

scala> Max(3) + Min(4)
<console>:14: error: Cannot find Semigroup type class for Product with Serializable
              Max(3) + Min(4)

Are monads really everywhere?

One thing that I have not yet investigated in further detail is how using monads compares to other patterns of abstraction. For instance, you can use monads in Clojure (the author Jim Duey actually wrote a whole series of blog posts covering monads), too, but in a quick initial search I observed that Clojure developers apparently use different constructs to achieve similar effects.

If you have some insights to share here, please feel free to reply to this post!

Summary

I hope this post contributes a little bit to the understanding of the rather abstract concepts of monoids and monads, and how you can put them to good practical use via tools such as Algebird, Scalding and SummingBird.

One of my lessons learned was that working with monoids and monads is a nice opportunity to read up on more formal concepts (category theory), and at the same time realize how they can be put to practical use in engineering, notably when doing large-scala data analytics.

On my side I want to thank the Twitter engineering team (@TwitterEng) not only for making those tools available to the open source community, but also for sparking my interest in the practical application of algebraic structures and category theory in general. Same shout-out for all the various people who wrote blog posts on the topic, or who shared their insights on places such as StackOverflow (see the reference section at the end of this article for a few of them). As I said there was a lot of new information to swallow – and in a short period of time – but the quest was worth it.

Many thanks! –Michael

References

Monads and monoids

I tried to categorize the references below into “easy” and “advanced” reads. Of course this is highly subjective, and your mileage may vary.

Easy reads:

Advanced reads:

SummingBird

Category theory

Speaking from my own experience I would say you do not need to understand the full details of category theory. The links above should contain all the information you need to gain enough understanding of monoids, monads and such that you can be productive in a short period of time. However I have used the references below to fill gaps that remained after reading through the other sources above, and I remember I did jump back and forth between the academic references below and the more hands-on resources above.

  • An Introduction to Category Theory, by Harold Simmons. As a novice to category theory I preferred this text over Category Theory for Computing Science (see below). Unlike the latter though the book of Simmons is not available for free.
  • Category Theory for Computing Science, by Michael Barr and Charles Wells, available as a free PDF. This seems to be a seminal work on category theory and worth the read if you are interested in the mathematical foundation of the theory in about 400 pages.
Interested in more? You can subscribe to this blog and follow me on Twitter.